QUESTÃO CERTA: Considere uma função de produção que utilize capital (K) e trabalho (L), estando as isoquantas dessa produção (Q) descritas na figura apresentada. A partir desses dados, julgue o item que se segue. A referida função de produção apresenta rendimentos constantes à escala.
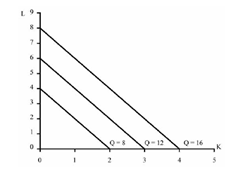
Quando o aumento dos fatores de produção em determinada escala resulta em aumento na produção na mesma escala, temos rendimentos constantes de escala. Como observado nos dados da questão.
QUESTÃO ERRADA: A função de produção em questão respeita a lei dos rendimentos marginais decrescentes.
Ao se tratar de isoquantas, supõe-se que estamos no longo prazo, ou seja, todos os insumos são variáveis.
No entanto a aplicabilidade da lei dos rendimentos marginais decrescentes restringe-se aos casos de curto prazo (pelo menos 1 insumo é fixo), daí o erro da questão.
Lei dos rendimentos marginais decrescente (David Ricardo): à medida que aumentamos o uso de determinado fator de produção, mantendo-se os outros insumos de produção constantes, chegamos a um ponto em que a produção adicional resultante começa a decrescer.
QUESTÃO CERTA: Constitui exemplo de rendimentos de escala crescentes a função de produção X = 0,5KL, em que X é a produção física total, K é a quantidade dos recursos de capital e L é a quantidade de trabalho.
Correta, pois, quando temos grau de homogeneidade maior que 1, o rendimento de escala é crescente. No caso da questão, temos os expoentes de K e L igual a 1, logo o grau de homogeneidade é igual 2. Isso se aplica, é claro, se estivermos na função Cobb-Douglas. Esse seu modo de fazer só não é vantajoso quando a cobb vem com expoente diferente de 1, aí é melhor apenas somar os expoentes,
Para rendimentos constantes de escala, um aumento de K e L em determinada proporção aumentará Q nessa mesma proporção.
Ex.: Situação 1) Q=4; K= 2; L=2 —> Dobrando K e L –> K=4; L=4 e, respeitando o princípio, teríamos Q=8 (mesma proporção)
Agora, para rendimentos crescentes de escala, um aumento de K e L em determinada proporção aumentará Q em proporção maior.
Aplicando na questão: X = 0,5.K.L –> X’ = 0,5.2K.2L –> X’=4.X Veja, portanto, que houve um aumento proporcionalmente maior.
QUESTÃO ERRADA: Os rendimentos de escala estão associados ao aumento na escala de produção da firma e ao fato de que, à medida que a empresa ampliar sua escala de produção, o seu custo médio de curto prazo também aumentará.
Os rendimentos de escala estão associados a variações nos fatores de produção apenas no LONGO prazo. Assim, nada se pode afirmar a respeito do desempenho do custo médio de curto prazo.
QUESTÃO ERRADA: Considerando a função de produção Cobb-Douglas descrita por f(x,y) = Axa yβ , em que x e y são os fatores de produção e a e β, os parâmetros, julgue o item subsequente. Se a tecnologia de produção tem rendimentos constantes à escala, então a produtividade marginal dos fatores é constante.
Podemos definir economias de escala tanto do ponto de vista tecnológico como dos custos (conceito mais “econômico”):
Economia de escala técnica ou tecnológica: quando a produtividade física varia com a variação de todos os fatores de produção;
Economia de escala pecuniária: quando os custos por unidade produzida variam com a variação de todos os fatores de produção.
QUESTÃO CERTA: A função de produção Cobb-Douglas de uma firma é dada por y = Kα Lβ , em que y representa a quantidade de produto que a firma consegue produzir para diferentes quantidades de capital K e trabalho L. Com base nessas informações, julgue o item subsequente. Se α + β = 1, a função de produção apresenta retornos constantes de escala.
O grau de homogeneidade das funções de produção:
Achando o grau de homogeneidade: basta somar os coeficientes “a” e “b” da função de Cobb-Douglas Q= K^α.L^β
Rendimentos constante de escala
(α +β)=1
Homogênea de grau 1
Um aumento de K e L em determinada proporção, Q aumentará nesta mesma proporção.
Pmg dos fatores de produção são estritamente decrescentes (curto ou longo prazo).
Aplica-se o Teorema de Euler
Rendimentos crescentes de escala (economia de escala)
(α +β)>1
Homogênea em grau maior que 1
Aumentos de K e L em determinada proporção provocam aumentos de Q numa proporção maior.
Rendimentos decrescentes de escala (deseconomia de escala).
(α +β)<1
Homogênea em grau menor que 1
Aumentos de K e L em determinada proporção provocam aumentos de Q numa proporção menor.