QUESTÃO CERTA: Considere que u(x1, x2) = 4×11/2 + 8×21/2 seja a função utilidade do consumidor, em que xi (p1, p2, w) é a demanda do consumidor em relação ao bem i, i = 1,2, p1 é o preço do bem 1, p2 é o preço do bem 2 e w é a riqueza do consumidor. Nessa situação, em relação ao comportamento do consumidor, é correto afirmar que a demanda marshalliana do consumidor pelo bem:
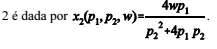
Utilizando o método dos multiplicadores de Lagrange:
*vou usar Y no lugar de X2 para ficar mais fácil a leitura
L = U(X,Y) + λ(RO)
U(X,Y) = 4X^0,5 + 8Y^0,5
RO => W = P1X + P2Y = 0 => W – P1X – P2Y = 0
L = 4X^0,5 + 8Y^0,5 + λ(W-P1X-P2Y)
Condições de 1a ordem:
-> derivada parcial de L em relação a X:
2X^-0,5 – λP1 = 0
λ = (2X^-0,5)/P1
-> derivada parcial de L em relação a Y:
4Y^-0,5 – λP2 = 0
λ = (4Y^-0,5)/P2
igualando os λ
(2X^-0,5)/P1 = (4Y^-0,5)/P2
…
Y = (4P1²X)/P2²
X = (P2²Y)/4P1²
Aplicando as equações acima na restrição orçamentária:
RO: P1X + P2Y = W
P1X + P2[(4P1²X)/P2²] = W
…
X = (P2W)/P1P2+4P1²
RO: P1X + P2Y = W
P1[(P2²Y)/4P1²) + P2Y = W
…
Y = (4P1W)/4P1P2+P2²
QUESTÃO ERRADA: Considerando a função utilidade U = 2x 0,4y 0,6 , com px = 1 e py = 6, em que pi é o preço do bem i e a renda do consumidor é igual a 50 unidades monetárias, julgue o seguinte item.
A demanda marshalliana do bem x é igual a 30/px.
Errado.
Em uma Cobb-Douglas do tipo U = x^a.y^b a demanda marshalliana do bem X é:
X = a/a+b.M/Px
Onde,
M = renda do consumidor
Px = preço do bem X
Com a = 0,4, M = 50 e Px = 1 a demanda marshalliana é igual a 20/Px.