QUESTÃO CERTA: É possível que haja rendimentos constantes de escala e produto marginal decrescente para uma dada tecnologia.
Trata-se da função cobb douglas. Achando o grau de homogeneidade: basta somar os coeficientes “a” e “b” da função de Cobb-Douglas Q= K^α.L^β
Rendimentos constante de escala (α +β)=1
Homogênea de grau 1
Um aumento de K e L em determinada proporção, Q aumentará nesta mesma proporção.
Pmg dos fatores de produção são estritamente decrescentes (curto ou longo prazo).
Teorema de Euler
Rendimentos crescentes de escala (economia de escala) (α +β)>1
Homogênea em grau maior que 1
Aumentos de K e L em determinada proporção provocam aumentos de Q numa proporção maior.
Rendimentos decrescentes de escala (deseconomia de escala). (α +β)<1
Homogênea em grau menor que 1
Aumentos de K e L em determinada proporção provocam aumentos de Q numa proporção menor.
Já o produto marginal decrescente tem a ver com a lei dos rendimentos marginais decrescentes: à medida que aumentamos o uso de determinado fator de produção, mantendo-se os outros insumos de produção constantes, chegamos a um ponto em que a produção adicional resultante começa a decrescer.
QUESTÃO ERRADA: Considerando a função de produção Cobb-Douglas descrita por f(x,y) = Axa yβ , em que x e y são os fatores de produção e a e β, os parâmetros, julgue o item subsequente: Se a + β > 0, a economia apresenta rendimentos crescentes à escala.
A economia apresenta rendimentos crescentes à escala quando a + β > 1.
QUESTÃO CERTA: Considerando-se um consumidor que possua uma função utilidade do tipo Cobb-Douglas, em que somente os bens x e y sejam consumidos, se o governo aumentar em 20% o imposto exclusivamente sobre o bem x, então, o consumidor maximizador: não alterará o consumo do bem y.
QUESTÃO ERRADA: Considerando a função utilidade U = 2x 0,4y 0,6 , com px = 1 e py = 6, em que pi é o preço do bem i e a renda do consumidor é igual a 50 unidades monetárias, julgue o seguinte item. O consumidor escolhe de forma ótima 25 unidades do bem x.
Inicialmente, vale notar que a função utilidade em questão é uma função Cobb-Douglas e que, além disso, o enunciado ainda nos deu a renda do consumidor. Utilizando a fórmula que mostra a quantidade ótima do consumidor, temos:
Q = 0,4 / 0,4+0,6 x 50 / 1 (renda / preço de “x”)
Resolvendo a equação, encontraremos que X = 20. Ou seja, a quantidade ótima do consumo de X é igual a 20 e não a 25, como afirma a questão.
QUESTÃO CERTA: Considerando a função utilidade U = 2x 0,4y 0,6 , com px = 1 e py = 6, em que pi é o preço do bem i e a renda do consumidor é igual a 50 unidades monetárias, julgue o seguinte item. O consumidor escolhe de forma ótima 5 unidades do bem y.
Vale o mesmo raciocínio que foi analisado na questão acima; no entanto, para o bem y. Utilizando a fórmula que mostra a quantidade ótima do consumidor, temos:
Y = 0,6 / 0,4+0,6 x 50 / 6 (renda / preço de y)
Resolvendo a equação, encontraremos que Y = 5 unidades.
QUESTÃO CERTA: Considerando a função utilidade U = 2x 0,4y 0,6 , com px = 1 e py = 6, em que pi é o preço do bem i e a renda do consumidor é igual a 50 unidades monetárias, julgue o seguinte item. O nível de satisfação ótimo do consumidor é superior a 17 unidades.
O nível de satisfação significa o valor da utilidade no ponto ótimo, isso pois não se faz nenhuma referência a unidades de bens, o que implica que é unidade de utilidade:
No ponto ótimo x=20 e y=5, aplicando na fórmula de utilidade:
U= 2 * 20 ^ 0,4 * 5 ^ 0,6 = 17,41
QUESTÃO CERTA: Determinada firma combina capital (K) e trabalho (L) por meio da função de produção Q = K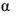
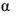
A função de Cobb-Douglas é homogênea de grau a+β, a função com retornos constantes de escala tem a+β=1. Logo, a PMg de L é igual a β(K^a).(L^(β-1)),ao somarmos os expoentes obtemos o valor = 0, logo a função é homogênea de grau zero. Questão correta.
QUESTÃO CERTA: Considerando uma função de produção Cobb-Douglas dada por y = Kα Lß , em que y indica o montante produzido de determinado bem para cada quantidade K de capital, e cada quantidade L de trabalho, julgue os itens subsequentes. Se r e w são, respectivamente, os preços do K e do L, então a combinação ótima desses insumos para determinado custo C se dá no ponto em que K/L = α/ß x w/r
Combinação ótima é quando a produção marginal do insumo se iguala ao preço real do insumo. Sendo P=o nível de preços, a=alfa, b=beta:
PMgK=r/P e PMgL=w/P
PMgK=dY/dK=a*K^(a-1)*L^b ; PMgL=dY/dL=b*K^a*L^(b-1)
Igualando as produções marginais aos preços reais, fica assim:
K=(a*K^a*L^b* P)/r ; L=(b*K^a*L^b*P)/w
Fazendo a divisão K/L, chega-se ao resultado do enunciado w/r=(a/b)*(w/r)