Função Utilidade Indireta do Consumidor (Cobb-Douglas)

QUESTÃO CERTA: Considere que a função utilidade do consumidor do tipo Cobb-Douglas seja expressa na forma 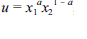, em que x₁ e x₂ são as quantidades, respectivamente, dos bens 1 e 2, α ∈(0,1) é um escalar e p₁ e p₂ são os preços dos bens 1 e 2 respectivamente.

Considerando que w seja a renda do consumidor, julgue o item que se segue, relativo à teoria do consumidor. A função utilidade indireta do consumidor é expressa

por .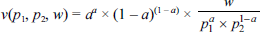

Como se calcular a função utilidade indireta do consumidor numa Coubb-Douglas: é a função de demanda do bem 1 elevada a potência do bem 1 multiplicada pela função de demanda do bem 2 elevada a potência do bem 2. Como assim? Já sabemos qual é a função do bem 1 que é:

Função de demanda do bem 1= aW/P1

Agora vou elevar essa função de demanda a potência do bem 1, logo:

[ a* W/P1 ] ^ a

a^a * [W/p1] ^a

a^a * [ W^ a / p1 ^a ]

Agora vou calcular a função de demanda do bem 2:

Função de demanda do bem 2= [X2/ X1+X2] * [ W/P2]

Função de demanda do bem 2= [1-a/ a+(1-a)] * [ W/P2]

Função de demanda do bem 2= (1-a) * [ W/P2]

Agora vou elevar essa função de demanda a potência do bem 2, logo:

{(1-a) * [ W/P2]} ^ ( 1-a)

(1-a) ^ ( 1-a) * [ W/P2] ^ ( 1-a)

(1-a) ^ ( 1-a) *  [W ^ ( 1-a) / P2 ^ ( 1-a)]

Agora vou multiplicar ambas, para encontrar a função utilidade indireta:

{ a^a * [ W^ a / p1 ^a ] } * { (1-a) ^ ( 1-a) *  [W ^ ( 1-a) / p2 ^ ( 1-a)] }

{ a^a* (1-a) ^ ( 1-a)} [ W^ a / p1 ^a ] * [W ^ ( 1-a) / p2 ^ ( 1-a)]

{ a^a* (1-a) ^ ( 1-a)} [ W^ a * W ^ ( 1-a) / p1 ^a * p2 ^ ( 1-a)]

Nesse em negrito: repete a base, e some os expoentes

{ a^a* (1-a) ^ ( 1-a)} * [ W ^ a+ ( 1-a) / p1 ^a * p2 ^ ( 1-a)]

{ a^a* (1-a) ^ ( 1-a)} * [ W ^ a+-a+1  / p1 ^a * p2 ^ ( 1-a)]

{ a^a* (1-a) ^ ( 1-a)} * [ W ^1  / p1 ^a * p2 ^ ( 1-a)]

{ a^a* (1-a) ^ ( 1-a)} * [ W  / p1 ^a * p2 ^ ( 1-a)]